HOW IT WORKS

MODULAR DESIGN

The construction system follows a modular design, so it is easier for you to modify the TCS, personalizing it to your needs. The goal is that you can build your own large hardware components, that you can develop your own structures and attach your own parts easily.

OCTET TRUSS STRUCTURE

Three tetrahedrons and two pyramids can form an octet truss structure to build plain walls.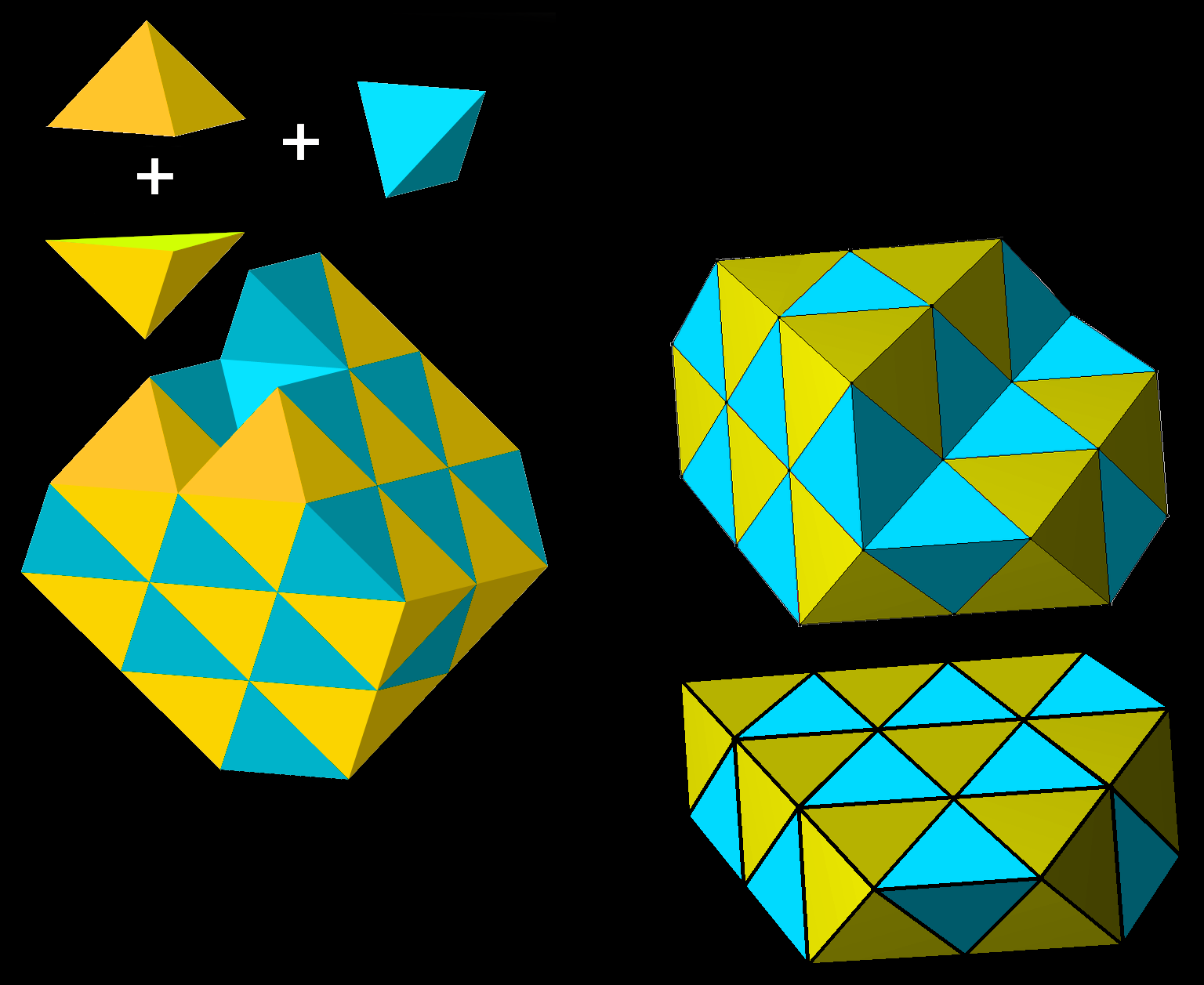

DIMENSIONS

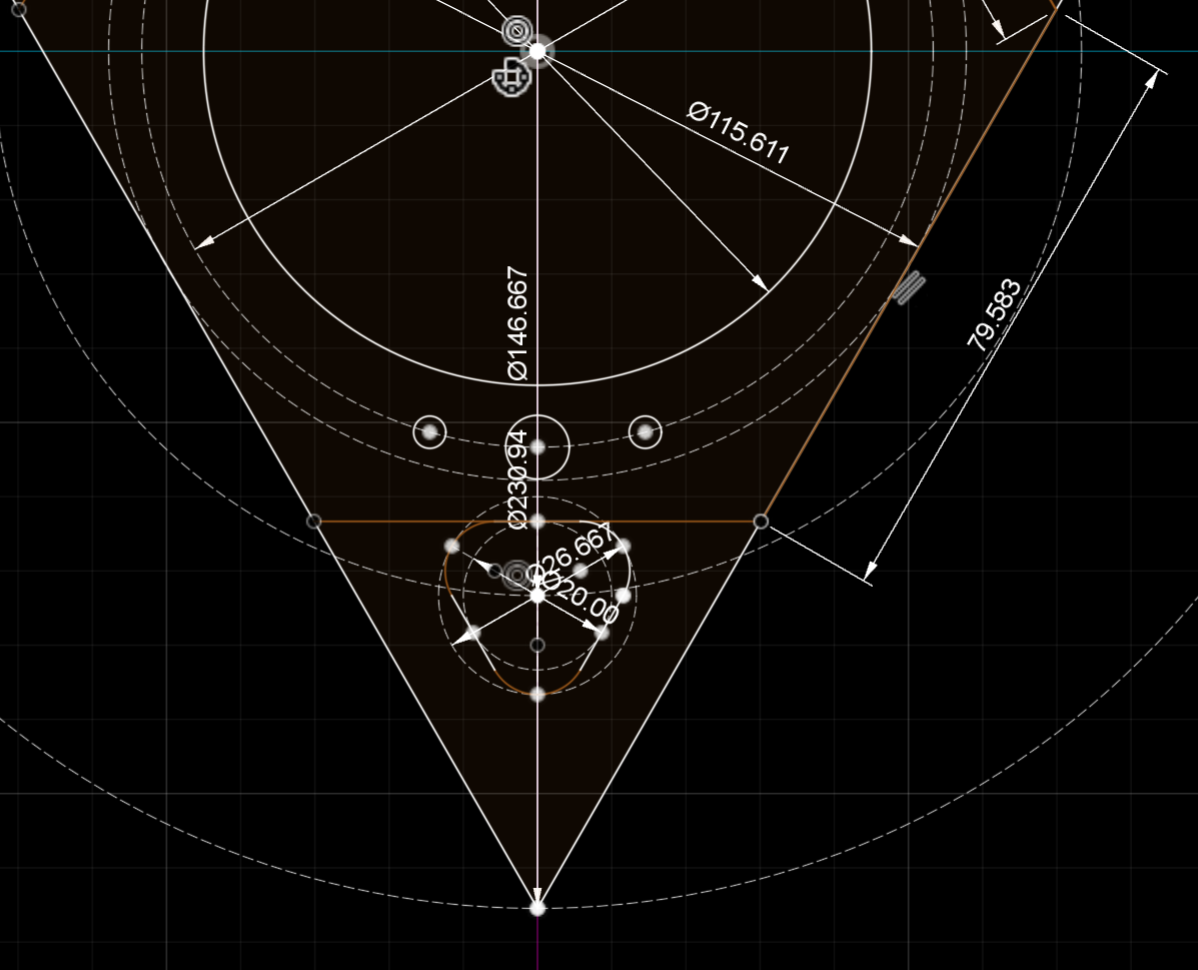
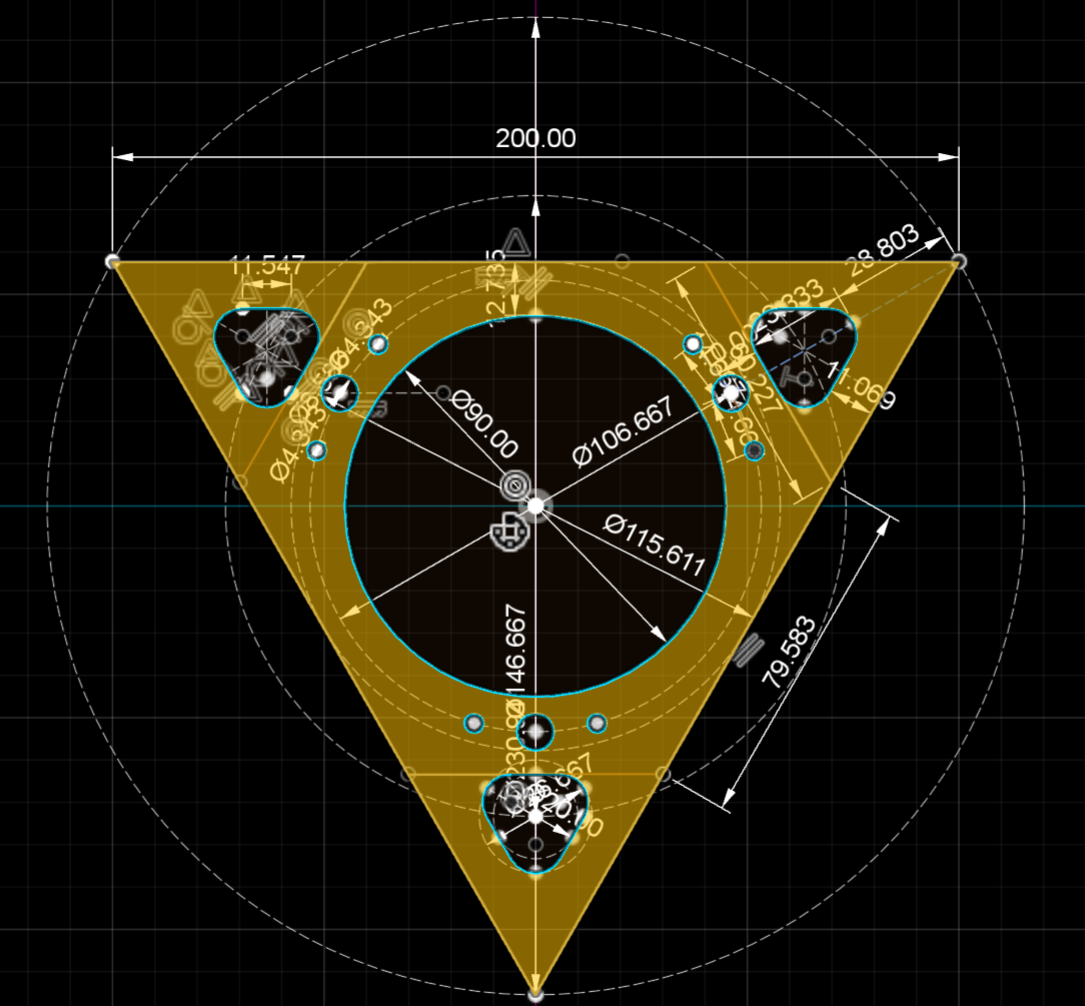
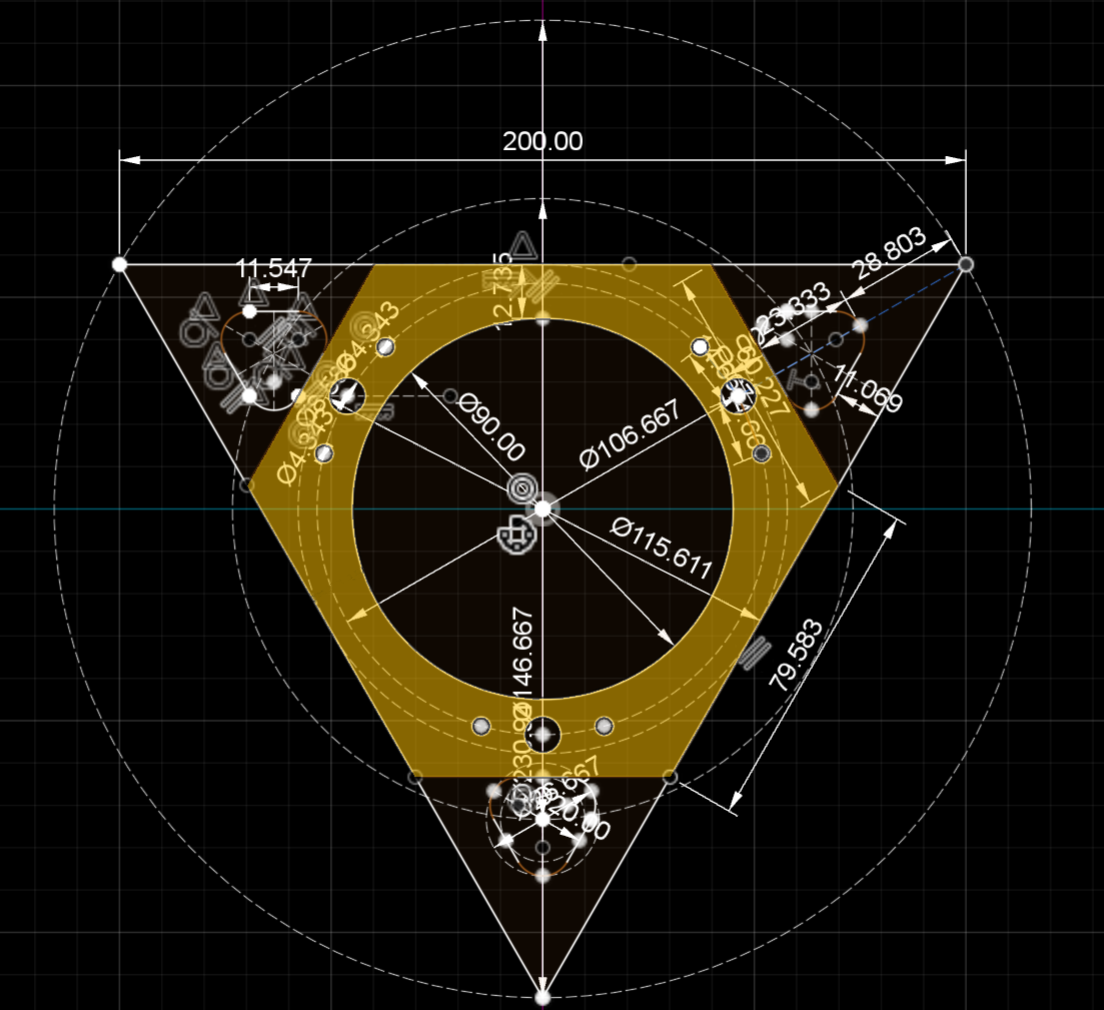
The following diagrams show the dimensions of the central connecting area of the TCS measured in mm.

The holes, their sizes and arrangements relative to each other can thus be found on the contact surfaces of the various components of the TCS. For example in the tetrahedron, the tetrahedron rounded, the pyramid, the pyramid less material and the pyramid rounded. The cover plates and plugs fit in accordingly.



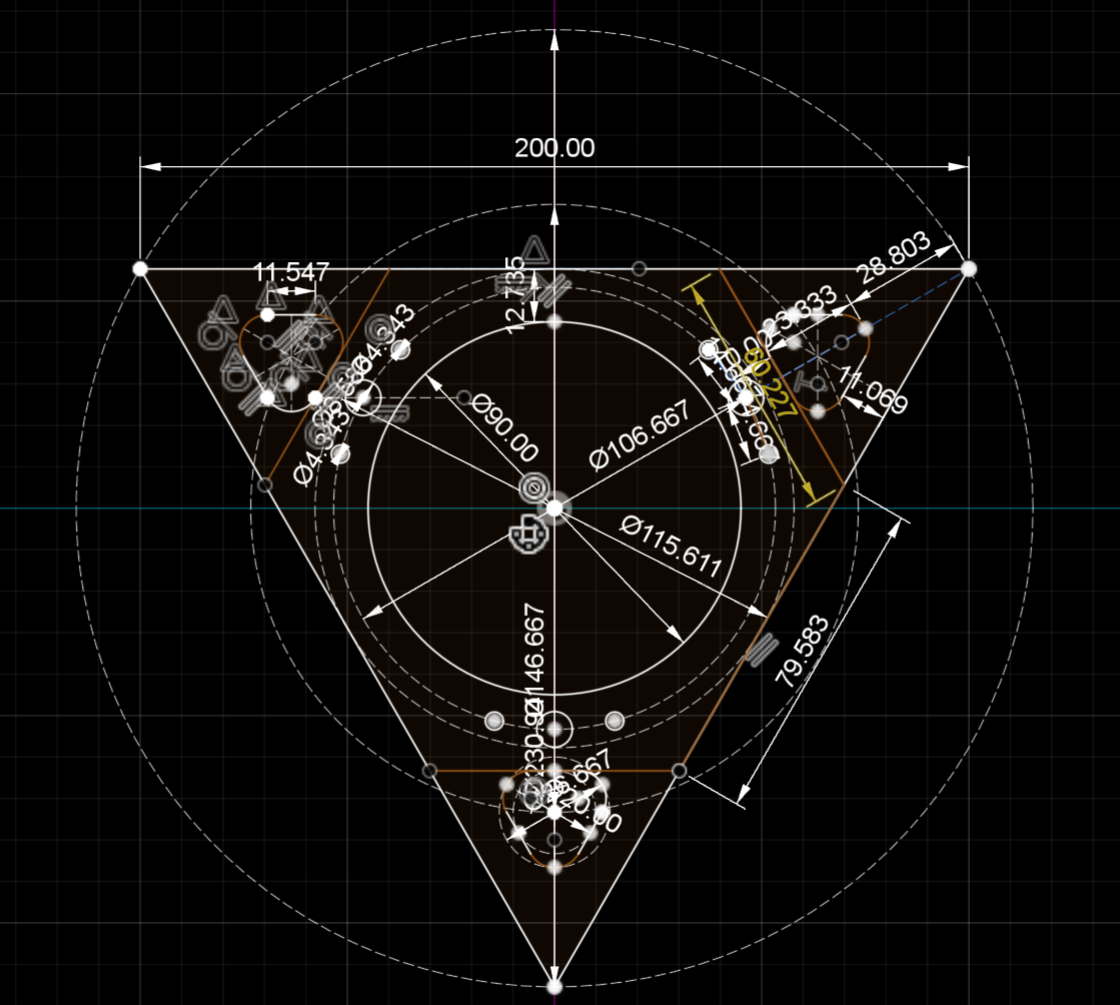
The top right corner has been enlarged to make the dimensions easier to read.



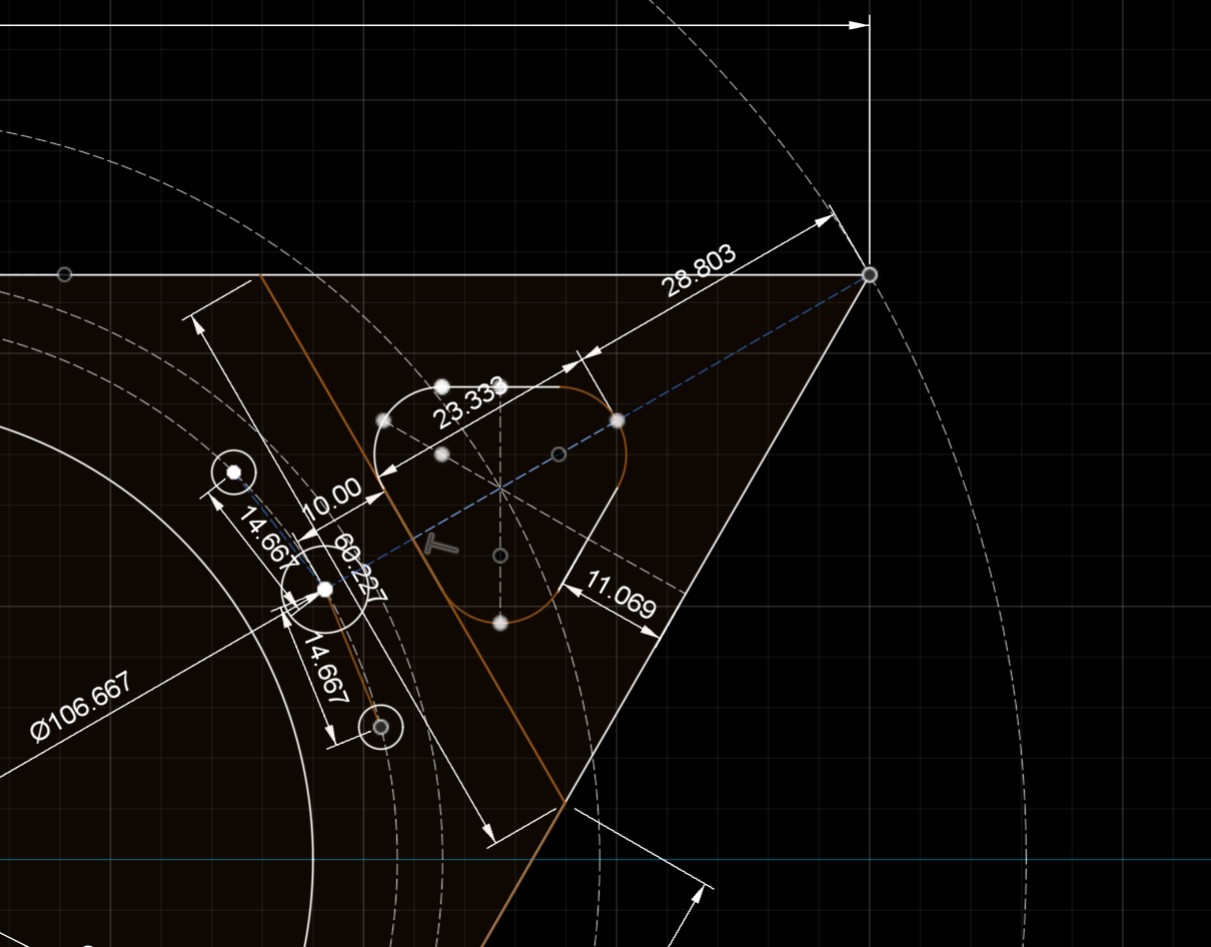
The top left corner has been enlarged.



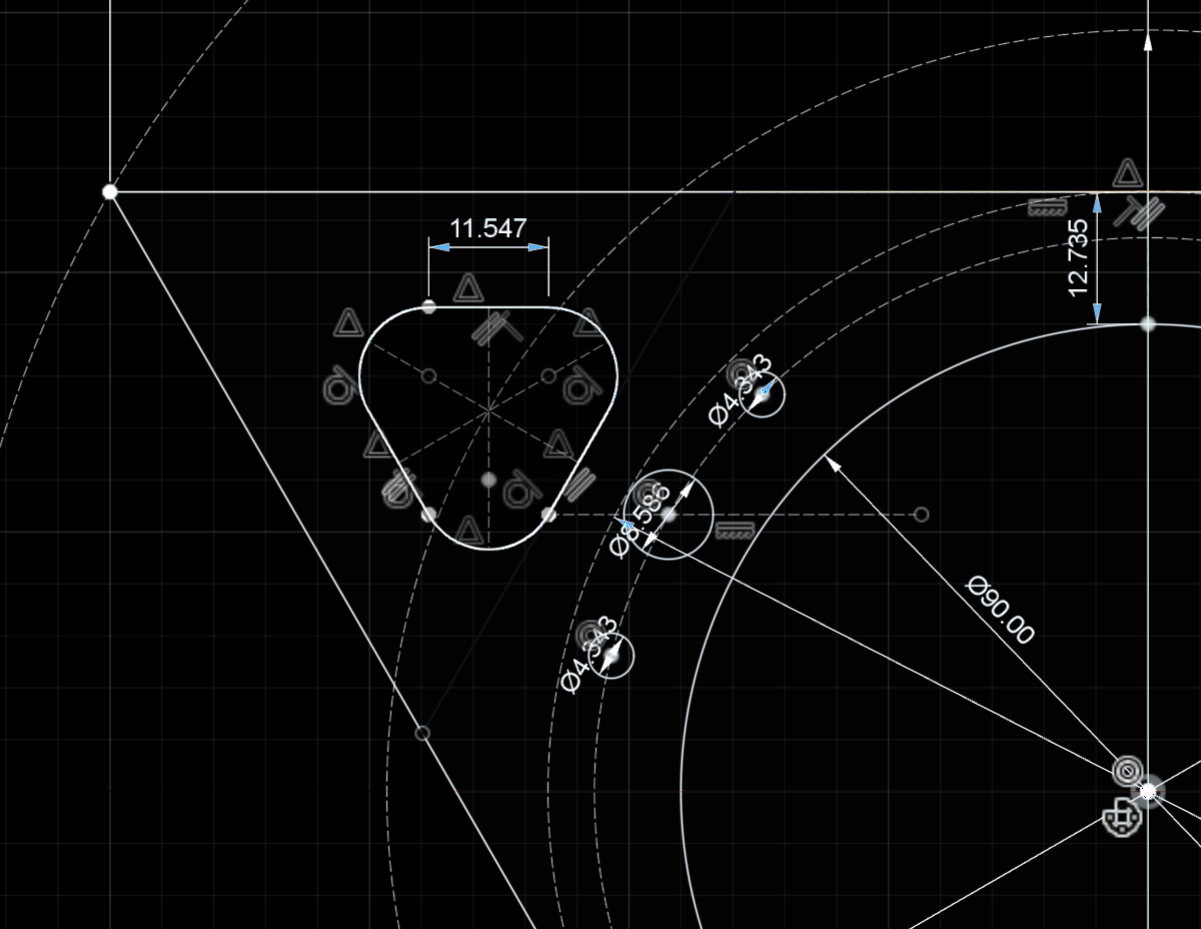
The bottom corner has been enlarged.



The normal tetrahedron uses the whole surface area.



The tetrahedron rounded only uses the main surface area of the tetrahedron and leaves out the corners.

GEOMETRIC CALCULATIONS

The following table presents the geometric calculations.

parameter	formula for square pyramid	formula for tetrahedron	value for square pyramid	value for tetrahedron
edge length	\(a\)	\(a\)	200mm	200mm
interior angle of equilateral triangle	\(60^\circ\)	\(60^\circ\)	\(60^\circ\)	\(60^\circ\)
volume	\(\frac{1}{3} a^2 h\)	\(\frac{\sqrt{2}}{12} a^3\)	\( \approx 94280.9\, \text{mm}^3 \)	\( \approx 47140.5\, \text{mm}^3 \)
surface area	\(a^2 + 2a\sqrt{\left(\frac{a}{2}\right)^2 + h^2}\)	\(\sqrt{3} a^2\)	\( \approx 80901.7\, \text{mm}^2 \)	\( \approx 69282.0\, \text{mm}^2 \)
circumsphere radius	\(\sqrt{\left(\frac{a}{2}\right)^2 + h^2}\)	\(\frac{a \sqrt{6}}{4}\)	\( \approx 158.1\, \text{mm} \)	\( \approx 122.5\, \text{mm} \)
insphere radius	\(\frac{a}{2\sqrt{2}}\)	\(\frac{a \sqrt{6}}{12}\)	\( \approx 70.7\, \text{mm} \)	\( \approx 49.0\, \text{mm} \)
base angle of isosceles triangles	\(\arctan\left(\frac{2h}{a}\right)\)	\(\arccos\left(\frac{1}{3}\right)\)	\( \approx 56.31^\circ \)	\( \approx 70.53^\circ \)
vertex angle of isosceles triangles	\(2 \arctan\left(\frac{h}{\frac{a}{2}}\right)\)	\(\arccos\left(\frac{1}{3}\right)\)	\( \approx 67.38^\circ \)	\( \approx 70.53^\circ \)
angle between base and isosceles triangles	\(\arctan\left(\frac{2h}{a}\right)\)	\(\arccos\left(\frac{1}{3}\right)\)	\( \approx 56.31^\circ \)	\( \approx 70.53^\circ \)
angle between isosceles triangles	\(2 \arctan\left(\frac{h}{\frac{a}{2}}\right)\)	\( \arccos\left(-\frac{1}{3}\right)\)	\( \approx 67.38^\circ \)	\( \approx 109.47^\circ \)
angle between edge and base	\(\arctan\left(\frac{h}{\frac{a}{2}}\right)\)	\(\arccos\left(\frac{1}{3}\right)\)	\( \approx 33.69^\circ \)	\( \approx 70.53^\circ \)
solid angle at base	\(2 \pi - 4 \arctan\left(\frac{\sqrt{2h^2 + a^2}}{a}\right)\)	\(3 \arccos\left(\frac{1}{3}\right)\)	\( \approx 4.63 \, \text{sr} \)	\( \approx 7.18 \, \text{sr} \)
solid angle at apex	\(4 \arctan\left(\frac{\sqrt{2h^2 + a^2}}{a}\right)\)	\(4 \arccos\left(\frac{1}{3}\right)\)	\( \approx 1.63 \, \text{sr} \)	\( \approx 4.84 \, \text{sr} \)
height	\(h = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{a \sqrt{3}}{2}\right)^2}\)	\(\frac{a \sqrt{2}}{\sqrt{3}}\)	\( \approx 141.42\, \text{mm} \)	\( \approx 115.47\, \text{mm} \)
volume to circumsphere volume ratio	\(\frac{volume}{\frac{4}{3} \pi \left(Circumsphere Radius\right)^3}\)	\(\frac{volume}{\frac{4}{3} \pi \left(Circumsphere Radius\right)^3}\)	\( \approx 0.016 \)	\( \approx 0.048 \)
sphericity	\(\frac{\pi^{1/3} (6 volume)^{2/3}}{Surface Area}\)	\(\frac{\pi^{1/3} (6 volume)^{2/3}}{Surface Area}\)	\( \approx 0.86 \)	\( \approx 0.94 \)

FORCE CALCULATIONS THEORY

SQUARE PYRAMID DIAGONAL STAB FORCES AND BASE FORCES
Assuming an edge length \(a = 200\, \text{mm}\) and a height \(h\), we can analyze the forces as follows: The vertical force \(F\) at the apex of the pyramid is distributed among the four diagonal edges. Each diagonal edge experiences a force \(F_d\). The force in each diagonal edge is calculated as: \[F_d = \frac{F}{\sqrt{2}}\] The base needs to support the vertical forces and distribute them among the corners. The reaction forces at the base are: \[R = \frac{F}{4}\] TETRAHEDRON EDGE FORCES
Assuming an edge length \(a = 200\, \text{mm}\), we can analyze the forces as follows: If a force \(F\) is applied at the apex of the tetrahedron, it is distributed equally among the three edges meeting at the apex. The force in each edge is calculated as: \[F_e = \frac{F}{3}\] STRESS IN THE STABS
Stress (\(\sigma\)) in a stab is calculated using the formula: \[\sigma = \frac{F}{A}\] (where \(A\) is the cross-sectional area of the stab)

STRAIN IN THE STABS
Strain (\(\epsilon\)) in a stab is calculated using the formula: \[\epsilon = \frac{\Delta L}{L}\] (where \(\Delta L\) is the change in length and \(L\) is the original length of the stab)

DEFORMATION
Deformation (\(\Delta L\)) can be calculated from the strain and original length: \[\Delta L = \epsilon \cdot L\] YOUNG'S MODULUS
Young's modulus (\(E\)) relates stress and strain: \[E = \frac{\sigma}{\epsilon}\]

FORCE CALCULATIONS PRACTICE

The following table presents the force calculations for a square pyramid.

parameter	formula	value
diagonal force \(F_d\)	\(F_d = \frac{F}{\sqrt{2}}\)	\(\approx 0.707F\)
reaction force \(R\)	\(R = \frac{F}{4}\)	\(0.25F\)
stress \(\sigma\)	\(\sigma = \frac{F}{A}\)	depends on cross-sectional area \(A\) (the tensile strength is about 55MPa to 70MPa for PLA)
strain \(\epsilon\)	\(\epsilon = \frac{\Delta L}{L}\)	depends on deformation \(\Delta L\) (the elongation at break is about 5% to 8% for PLA)
deformation \(\Delta L\)	\(\Delta L = \epsilon \cdot L\)	depends on strain \(\epsilon\)
Young's modulus \(E\)	\(E = \frac{\sigma}{\epsilon}\)	material specific (about 2.7 to 3.9 for PLA)

The following table presents the force calculations for a tetrahedron.

parameter	formula	value
edge force \(F_e\)	\(F_e = \frac{F}{3}\)	\(\approx 0.333F\)
stress \(\sigma\)	\(\sigma = \frac{F}{A}\)	depends on cross-sectional area \(A\) (the tensile strength is about 55MPa to 70MPa for PLA)
strain \(\epsilon\)	\(\epsilon = \frac{\Delta L}{L}\)	depends on deformation \(\Delta L\) (the elongation at break is about 5% to 8% for PLA)
deformation \(\Delta L\)	\(\Delta L = \epsilon \cdot L\)	depends on strain \(\epsilon\)
Young's modulus \(E\)	\(E = \frac{\sigma}{\epsilon}\)	material specific (about 2.7 to 3.9 for PLA)

Sounds good? Maybe you want to take a look at the used PARTS and the BUILDING INSTRUCTIONS.